Verbalizing Business Rules (Part 1)
Although business rules may be implemented in many ways, they should first be specified at the conceptual level, using concepts and language easily understood by the business domain experts who are required to validate the rules. Business rules come in many varieties, such as constraints and derivation rules, and may be specified using graphical and/or textual languages. The focus of this initial series of articles is on expressing business rules in a high-level, textual language. This particular article identifies some criteria for a business rules language, and discusses how to verbalize some basic constraints.
Some Basic Terminology
Before discussing language criteria, let's define some terms. A proposition is what it is that is asserted when a declarative sentence is uttered, and is always true or false. The same proposition may be asserted by different sentences. For example, when uttered in normal circumstances the following three sentences express the same (true) proposition:
- Honshu is an island of Japan.
- Honshu is a Japanese island.
- Honshu wa Nihon no shima desu.
In information modeling, propositions should be stated in a way that exposes identification schemes, e.g.,
The Island named 'Honshu' is part of the Country named 'Japan.'
A predicate is a proposition with object-holes in it. A declarative sentence consists of a predicate symbol (e.g., is part of ) applied to a sequence of one or more object terms (e.g., "The Island named 'Honshu'" "The Country named 'Japan'"). An object type is a kind of object, e.g., Island, Country. A fact type includes predicate and object type(s) but not instances, e.g., Island is part of Country. A predicate-role is a part played by an object in a predicate. In the context of a predicate, a predicate-role is simply called a role. The number of roles in a predicate is called its arity.
Table 1 includes some examples of predicates with arities in the range 1..4.
Each role corresponds to an object placeholder (depicted here as an ellipsis "
")
in the predicate. Here predicates are displayed in mixfix notation,
allowing object terms to be placed in a sentence at any position. Higher order
predicates (quinary etc.) are also possible.
|
Fact Type |
Predicate |
Arity |
Arity Descriptor |
| Person smokes | smokes |
1 |
Unary |
| Person was born in Country | was born in |
2 |
Binary |
| Person played Sport for Country | played for |
3 |
Ternary |
| Person introduced Person to Person on Date | introduced to on |
4 |
Quaternary |
Language Design Criteria
In [[2], sec. 3.1], the following criteria are suggested for evaluating the suitability of a conceptual modeling language: expressibility (what can be expressed?); clarity (ease of understanding); simplicity and orthogonality (avoid unneeded concepts, minimize inter-concept dependencies, allow expressions wherever their values are legal); semantic stability (minimize the impact of change); semantic relevance (ignore implementation details); validation mechanisms (support ways for domain experts to validate the model); abstraction mechanisms (provide ways of hiding detail); and formal foundation (logical grounding).
With specific reference to a textual language for business rule expression, the following criteria seem to be the most essential:
- expressibility the language must be capable of expressing a wide range
of business rules
- clarity rules in the language must be understandable by non-technical
domain experts
- formality rules in the language must be unambiguous, and should ideally be executable
An adequate coverage of the language clarity criterion implies the following desirable properties:
- any-arity the language should directly support predicates of any arity
- localizability the language constructs should be easily expressed in different native languages
Supporting predicates of any arity allows domain experts to verbalize the rules
directly in terms of the way they think. This makes it much easier for them
to understand and validate the rules. It is always possible to reformulate
unary, ternary, and higher arity predicates in terms of binary predicates, but this
can make it harder for the subject matter experts to comprehend the rules.
Some rules are hard enough to get a grip on in the first place. There is no
excuse for imposing a binary straightjacket on the domain expert that forces them
to recast a fact type they would normally verbalize as a quaternary in terms of a
binarized equivalent (e.g., a binary nested within a binary nested with a binary).
Similarly, we should not force domain experts to recast unary facts such as "Country
'US' is large" in terms of Boolean attribute assignments (e.g., US : Country.isLarge = True).
Once we accept that predicates of any arity must be supported, and that sentences
should be able to be verbalized naturally, it follows that mixfix notation
must be supported. In Table 1, the "
smokes" predicate is prefix, and the "
was born in
" predicate is infix, but the "
played
for
" and "
introduced
to
on
" predicates require
mixfix because they have more than two object placeholders. Although prefix
or postfix notation could be used, such as PlayedFor(X,
Y, Z), this would be unnatural for non-technical people.
The localizability criterion provides yet another reason for mixfix notation, since even for binary predicates, the verb-phrase need not occur in the infix position. For example, verbs are usually placed last in Japanese, and are usually placed first in Tongan. Having made this point, I will restrict discussion of business rules textual languages to those based on English.
It can be useful to provide a simple, informal verbalization of business rules, so long as this verbalization is unambiguous to the domain expert who has to validate the rules. The RuleSpeak sentence templates[5] provide useful advice on how to do this. To exploit the benefits of model-driven development however, business rules should be expressed in a formal language, so that they can be automatically transformed into executable code. Ideally, this formal language should at the same time be conceptual, so that it can serve for communication and validation with domain experts, as well as being executable. The following discussion is confined to consideration of such a language.
Simple Mandatory and Uniqueness Constraints
Business rules are model elements (e.g., constraints or derivation rules) that
apply to other model elements (e.g., fact types) that have already been defined.
The model may be specified textually or graphically using a variety of notations.
Figure 1 graphically depicts a binary relationship (orbiting)
between two entity types (Moon
and Planet) using:
(a) the Entity Relationship (ER) notation popularized by Richard Barker,
(b) the Unified Modeling Language (UML) notation,
(c) the Object-Role Modeling (ORM) notation, and
(d) a simple Fact Model notation.
Here the fact model notation merely shows the binary fact type without constraints (these rules are to be specified separately). Each of the other notations displays both the fact type and its associated constraints. The constraints indicate that each moon orbits exactly one (at least one and at most one) planet, and that a planet is orbited by zero or more moons.
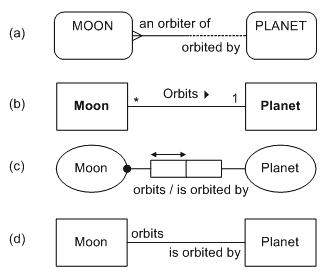
Figure 1. An n:1 association in (a) Barker ER, (b) UML, (c) ORM and (d) Fact Model notations.
To specify that each moon orbits at least one planet, both Barker ER and ORM use a mandatory role constraint. Barker ER depicts a role as one half of a relationship line, whereas ORM uses a role box. To indicate that a role is mandatory or optional, Barker ER uses a solid or dotted line respectively. In ORM, a role is optional unless it has been assigned a mandatory constraint (depicted graphically as a solid dot).
To indicate the n:1 cardinality of the Moon orbits Planet relationship,
Barker ER uses a single line end for "one" and crows-foot for "many."
ORM instead uses a uniqueness constraint depicted as an arrow-tipped bar over
the role(s) to which it applies. As shown later, ORM allows populated fact
tables to be associated with fact types, with each role corresponding to a table
column. A uniqueness constraint over a role (or role set) indicates that each
instance in the population of that role (or role set) is unique. The lack of
a uniqueness constraint indicates that an instance may occur there more than once.
Unlike Barker ER and ORM, the UML approach combines the separate
concepts of mandatory and cardinality/uniqueness constraints into a single multiplicity
constraint (e.g., '0..1' for at
most one, '1' or '1..1'
for exactly one, and '0..*' or
'*' for zero or more). Although
this multiplicity concept works fine for binary associations, it breaks down in a
number of ways for n-ary associations. For example, you can't use multiplicity
to specify that just one role of a ternary association is mandatory (see [3] for a detailed discussion of this and other problems
with UML). For such reasons, we will ignore UML for the rest of this article.
To enable association optionality and cardinality settings to be verbalized, Barker [[1], p. 3-5] recommends the following naming discipline for relationships. Let A R B denote an infix relationship R from entity type A to entity type B. Name R in such a way that each of the following four patterns results in an English sentence:
Each A (must | may) be R (one and only one B | one or more B-plural-form)
Use "must" or "may" when the first role is mandatory or optional respectively. Use "one and only one" or "one or more" when the cardinality on the second role is one or many respectively. For example, the optionality/cardinality settings in Figure 1(a) verbalize as:
Each Moon must be an orbiter of one and only one Planet.
Each Planet may be orbited by one or more Moons.
This verbalization convention is good for basic mandatory and uniqueness constraints
on infix binaries. So long as the user follows the naming discipline, and pluralization
can be automated (e.g., House
to/from Houses, Mouse to/from Mice),
these rules may be regarded as formal and executable.
Overall however, the Barker ER approach is too restrictive, because (a) it handles only binary associations, and (b) while it does include a few other graphical constraints, it provides no rules for verbalizing these in a textual language. In contrast, ORM applies to predicates of any arity, and covers many more kinds of constraint both graphically and textually, with no need for pluralization.
Let's see how an ORM textual language might cater for the simple mandatory and
uniqueness constraints in Figure 1(c). Later articles will investigate more
complex cases. For discussion purposes, the orbital
fact type is reproduced in Figure 2, along with another fact type about planets.
Reference schemes for each object type are shown in parenthesis, and sample fact
tables are also provided. The orbital
fact table is significant with respect to uniqueness constraints: its first
column values are unique, and its second column contains duplicates, clearly showing
the n:1 nature of the association.
The planetary radius table is only partly significant with respect to uniqueness
constraints, because its column values are unique for both roles, suggesting a 1:1 association. A domain expert
however can confirm that it is possible for two planets to have the same radius.
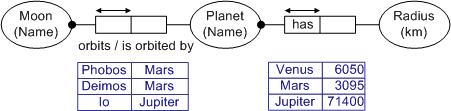
Figure 2. Two fact types with sample populations
Any constraint may be verbalized in both positive and negative form. The
uniqueness constraint on the first role of the fact type Moon
orbits Planet may be verbalized in thus:
Each Moon orbits at most one Planet. -- positive form It is impossible that the same Moon orbits more than one Planet. -- negative form
The positive form of a constraint can be illustrated by satisfying populations, as in Figure 2. The textual rule introduces the quantifiers each, and at most one, but leaves the fact type verbalization unaltered.

These quantifiers capture basic logical concepts that are found in all natural languages, so this approach is localizable.
The negative form of a constraint specifies what states are ruled out by the constraint, and can be illustrated by a counter-example that violates the constraint. For example, adding the fourth row to the fact table in Figure 3 results in a population where the same moon (Io) orbits two planets (Jupiter and Mars). This duplicate value in the first column violates the uniqueness constraint on that column. Use of counter-examples is a powerful way to check whether a constraint really does apply.
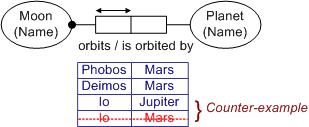
Figure 3. A counter-example shows how to violate the uniqueness constraint.
The absence of a constraint may be clarified by a default verbalization. For example, the absence of a uniqueness constraint on the second role of Moon orbits Planet may be verbalized explicitly thus:
It is possible that the same Planet is orbited by more than one Moon. -- default
The population illustrates this possibility (Mars has two moons). Negative and default verbalizations involve use of logical operators (not, possibly), correlation (the same), and quantifiers (e.g., more than one) that have corresponding representations in various natural languages.
The mandatory constraint on the first role of Moon orbits Planet may be verbalized in positive or negative form thus:
Each Moon orbits some Planet. -- positive form Each Moon orbits at least one Planet. -- positive form (an alternative for the existential quantifier) It is impossible that some Moon orbits no Planet. -- negative form (long version) No Moon orbits no Planet. -- negative form (shortversion)
The absence of a mandatory constraint on the second role of Moon orbits Planet may be stated explicitly by the following default verbalization. The combined population of the two tables in Figure 2 illustrates this possibility (Venus has no moons).
It is possible that some Planet is orbited by no Moon. -- default
If a role has both a simple uniqueness and simple mandatory constraint, both constraints may be combined in a single verbalization by using "exactly one" to abbreviate "at least one and at most one." For example, the constraints on the orbital fact type may be succinctly stated thus:
Each Moon orbits exactly one Planet. -- combined form
This may be formalized using Stephen Kleenes exactly-one quantifier thus:

The ORM constraint verbalization techniques discussed so far may be applied to binary associations in other approaches such as ER and UML as well. However the real benefits of these techniques are best appreciated when applying constraints to n-ary associations, as will be discussed in the next article in this series.
References
[1] R. Barker, CASE*Method: Tasks and
Deliverables, Addison-Wesley, Wokingham, England, 1990. ![]()
[2] T.A. Halpin, Information Modeling and Relational
Databases, Morgan Kaufmann, San Francisco, 2001. ![]()
[3] T. A. Halpin, 'Augmenting UML with Fact Orientation,'
Proc. UML Workshop, HICSS-34 Conference, IEEE, 2001. Available
online at http://www.orm.net/pdf/HICSS.pdf.
![]()
[4] Object Management Group, Unified Modeling Language (UML) Specification - Version 1.4, 2001. Available online at http://www.omg.org/technology/documents/formal/uml.htm.
[5] R. G. Ross & G. S. W. Lam, RuleSpeak Sentence
Templates: Developing Rules Statements Using Sentence Patterns, Business
Rule Solutions, 2001. Available online at www.BRSolutions.com. ![]()
# # #
About our Contributor:
Online Interactive Training Series
In response to a great many requests, Business Rule Solutions now offers at-a-distance learning options. No travel, no backlogs, no hassles. Same great instructors, but with schedules, content and pricing designed to meet the special needs of busy professionals.











How to Define Business Terms in Plain English: A Primer
How to Use DecisionSpeak™ and Question Charts (Q-Charts™)
Decision Tables - A Primer: How to Use TableSpeak™
Tabulation of Lists in RuleSpeak®: A Primer - Using "The Following" Clause
Business Agility Manifesto
Business Rules Manifesto
Business Motivation Model
Decision Vocabulary
[Download]
[Download]
Semantics of Business Vocabulary and Business Rules